Problem 55
Reconstruct bicyclic quadrilateral \(ABCD\) with its incenter \(I\), point \(E\) of intersection of tangents to the circumcircle at \(A, C\) and point \(F\) of intersection of tangents to the circumcircle at \(B, D\).
XXI Geometrical Olympiad in Honor of I.F. Sharygin, final round, 9th grade, problem 8
Tags: quadrilateral circles incircle circumcircle construction
Solution
First we prove two lemmas.
Lemma 1. \(EI\parallel BD\), \(FI\parallel AC\).
Proof. We may assume that \(AB\ge AD\). Note that \[\angle AIC=\angle IAB+\angle ICB+\angle B=90^\circ+\angle B=180^\circ -\frac{\angle AEC}{2},\] consequently \(E\) is the circumcenter of \(AIC\). Hence \begin{align*} \angle (IE,AC) &=\angle EIC+\angle ICA = 90^\circ - \angle IAC + \angle ICA \\ &=90^\circ-\frac{\angle BAC-\angle CAD}{2}+\frac{\angle BCA-\angle ACD}{2} =\frac{\overset{\frown}{BC} + \overset{\frown}{AD}}{2} =\angle (BD,AC) \end{align*} и \(EI\parallel BD\). Similarly \(FI\parallel AC\).
Lemma 2. Let \(AC\cap EF=\{K\}\), \(BD\cap EF=\{L\}\). Then \(\angle EIK= \angle FIL=90^\circ\).
Proof. Let \(O\) be the circumcenter of \(ABCD\), \(OI\cap EF=\{P\}\) (figure 1). By lemma 1 \(EI\parallel BD\perp OF\), \(FI\parallel AC\perp OE\), thus \(I\) is the orthocenter of \(OEF\) and \(OI\perp EF\). As we showed in the proof of the above lemma, \(E\) is the circumcenter of \(AIC\). Hence the circumcircles of \(AIC\) and \(IEP\) touch each other. On the other hand, \(A, C, P\) lie on the circle with diameter \(OE\). Hence \(K\) is the radical center of circumcircles of \(ACE, IPE, AIC\) and \(KI\) is the radical axis of the latter two, whence \(\angle EIK=90^\circ\). Similarly \(\angle FIL=90^\circ\).
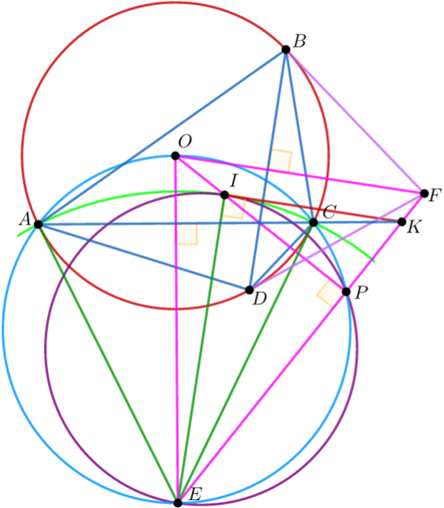
From the lemmas follows this construction:
- draw a line through \(I\), perpendicular to \(EI\) and mark the point \(K\) of its intersection with \(EF\); similarly construct the point \(L\),
- draw the lines \(k\) и \(l\) through \(K\) and \(L\), parallel to \(IF\) and \(IE\), respectively,
- construct the orthocenter \(O\) of \(EFI\),
- construct the circle with diameter \(OE\) and mark the points \(A\) and \(C\) of its intersection with \(k\); similarly construct the points \(B\) and \(D\).