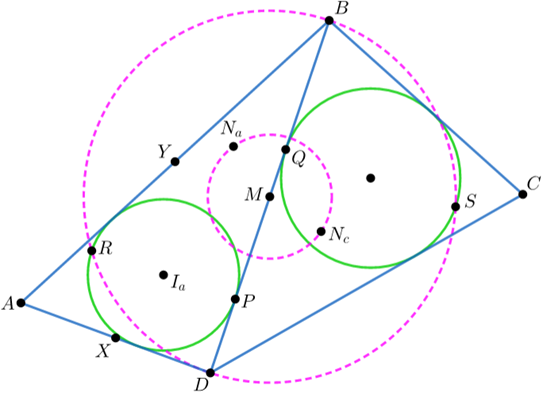
Problem 57

A quadrilateral \(ABCD\) is given in which \(AB+AD=CB+CD\). Circles \(\omega_A\) and \(\omega_C\) inscribed in \(ABD\) and \(CBD\) touch \(BD\) in points \(P\) and \(Q\), respectively. Points \(R\) and \(S\) are diametrically opposite to \(P\) and \(Q\) in \(\omega_A\) and \(\omega_C\), respectively. Prove that the points \(B, R, D, S\) are concyclic if and only if the Nagel points of \(ABD\) and \(CBD\) are equidistant from the midpoint of \(BD\).

XXVI Kolmogorov Cup, individual olympiad, senior group, conclusion, problem 7

Note. In the olympiad students were asked to prove the implication only in one direction.

Tags: triangle circles incircle Nagel point

Solution

Denote \(DA=x,AB=y,BC=z,CD=t,DB=u,x+y=z+t=p,x+y+u=2q,RP=2r_a,QS=2r_c\). First we prove the following lemmas․

Lemma 1. We have \[\angle BRD=90^\circ \iff p/u=5/3;\] \[\angle BRD>90^\circ \iff p/u<5/3;\] \[\angle BRD<90^\circ \iff p/u>5/3\] (clearly all this is true for \(\angle BSD\) as well).

Proof. Let \(M\) be the midpoint of \(BD\). We have \(MP=\dfrac{|x-y|}{2},r_a=\sqrt{\dfrac{(q-x)(q-y)(q-u)}{q}}\), thus \[\angle BRD=90^\circ \iff RM^2=MB^2 \iff MP^2+PR^2=MB^2 \iff 4r_a^2=(q-x)(q-y) \iff 4(q-u)=q\iff p/u=5/3.\] Using the equivalences \(\angle BRD>90^\circ \iff RM < BM\) and \(\angle BRD<90^\circ \iff RM>BM\) (if the side of a triangle is shorter than half the median towards it, then the angle in front of that side is acute; and vice versa) and the above judgement we will prove the other two parts of the lemma.

Lemma 2. Let \(N_a\) and \(N_c\) be the Nagel points of triangles \(BAD\) and \(BCD\), respectively. Then \(MN_a=MN_c\iff p/u=5/3\).

Proof. Let \(X\) and \(Y\) be the midpoints of \(DA\) and \(AB\), respectively, \(I_a\) be the incenter of \(BAD\). Since \(I_a\) is the Nagel point of \(XYM\), we have \(BN_a^2=4XI_a^2=4(r_a^2+(u-y)^2/4)\). Similarly \(DN_a^2=4YI_a^2=4(r_a^2+(u-x)^2/4)\). Applying the median length formula for triangle \(BN_a D\) we get \[4MN_a^2=2(BN_a^2+DN_a^2 )-BD^2=2(8r_a^2+(u-y)^2+(u-x)^2 )-u^2.\] Similarly \[4MN_c^2=2(8r_c^2+(u-z)^2+(u-t)^2 )-u^2.\] Hence \[MN_a=MN_c\iff 0=2(MN_a^2-MN_c^2 )\iff 0=8(r_a^2-r_c^2 )+(u-x)^2+(u-y)^2-(u-z)^2-(u-t)^2.\] Inserting \(2q=p+u, r_a^2=(q-x)(q-y)(q-u)/q\) and \(r_c^2=\dfrac{(q-z)(q-t)(q-u)}{q}\) we get that the last equality is equivalent to \[0=4\dfrac{q-u}{q}-1 \iff \dfrac{p}{u}=\dfrac 5 3.\]

Back to our problem. According to lemma 1, if \(\dfrac p u>\dfrac 5 3\) or \(\dfrac p u< \dfrac 5 3\) then \(\angle BRD+\angle BSD<180^\circ\) and \(\angle BRD+\angle BSD>180^\circ\), respectively, i.e. in both cases the points \(B,R,D,S\) are not concyclic. Thus concyclicity of \(B,R,D,S\) is equivalent to the condition \(\dfrac p u=\dfrac 5 3\), which, according to lemma 2, is equivalent to \(MN_a=MN_c\).